The y = kx calculator is an essential tool for anyone dealing with linear relationships. It helps users understand and visualize how changes in one variable affect another when they are directly proportional. This calculator not only supports academic learning but also assists professionals in fields such as physics and economics where such relationships are common.
Functionality of y kx Calculator
Using the calculator is straightforward:
- Input the constant of proportionality (k), which defines how much one variable affects another.
- Enter the value for x (independent variable).
- The calculator computes y (dependent variable), illustrating the outcome of the equation y = kx.
Formula
Expression:
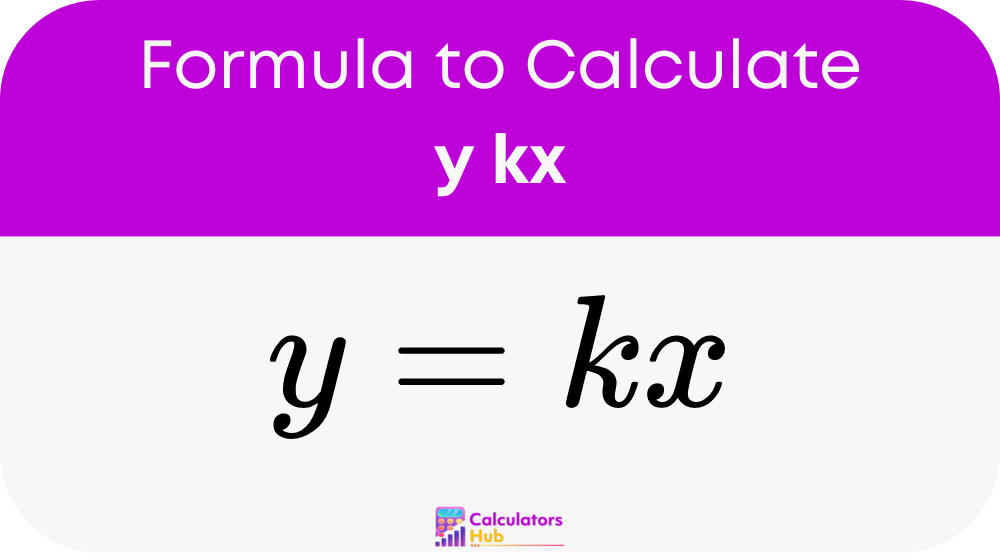
- y: This represents the dependent variable, calculated based on x and k.
- k: Known as the constant of proportionality, k determines how y changes with x.
- x: The independent variable, which you can freely adjust to see different outcomes for y.
Key Characteristics
- The equation’s graph is a straight line through the origin, showing uniformity in proportional change.
- A positive k means y increases with x, while a negative k means y decreases as x increases, showcasing the inverse relationship.
Table of Common Calculations for y = kx
| k (Constant of Proportionality) | x (Independent Variable) | y (Dependent Variable) = kx | Context Example |
|---|---|---|---|
| 1 | 1 | 1 | Unit price = 1, Quantity = 1 |
| 1 | 10 | 10 | Unit price = 1, Quantity = 10 |
| 10 | 1 | 10 | Unit price = 10, Quantity = 1 |
| 10 | 10 | 100 | Unit price = 10, Quantity = 10 |
| -1 | 1 | -1 | Unit deduction = 1, Quantity = 1 |
| -1 | 10 | -10 | Unit deduction = 1, Quantity = 10 |
| 0.5 | 2 | 1 | Half per unit, Two units |
| 0.5 | 20 | 10 | Half per unit, Twenty units |
| 2 | 5 | 10 | Double per unit, Five units |
| 2 | 50 | 100 | Double per unit, Fifty units |
| 5 | 20 | 100 | Price per unit = 5, Quantity = 20 |
| 100 | 1 | 100 | Rate = 100, Time = 1 (e.g., speed) |
| 100 | 10 | 1000 | Rate = 100, Time = 10 (e.g., speed) |
| 3.6 | 10 | 36 | Rate = 3.6 (kJ/min), Time = 10 min |
| 0.1 | 100 | 10 | Rate = 0.1, Distance = 100 |
| 20 | 5 | 100 | Speed = 20 km/h, Time = 5 h (distance) |
| 15 | 2 | 30 | Speed = 15 m/s, Time = 2 s (distance) |
| -0.5 | 100 | -50 | Deduction rate = 0.5, Quantity = 100 |
Examples of y kx Calculator
Sample Calculations
- Financial Calculation:
- If k = 0.05 (interest rate per year) and x = 10 (years), then y = 0.5, showing the total interest accumulated over the period.
- Physical Calculation:
- For a constant velocity (k = 90 km/h) traveling for 2 hours (x = 2), y = 180 km, showing the distance covered.
Most Common FAQs
This constant (k) defines the rate at which the dependent variable (y) changes in response to the independent variable (x). It remains constant throughout the relationship, ensuring a predictable and steady output.
Absolutely, y equals zero when x is zero in the y = kx equation, because the line representing the relationship passes through the origin, signifying no change when no input is provided.
The choice depends on the specific application:
In business, k could represent unit cost, with x being quantity.
In physical sciences, k might be a rate (like speed), with x representing time.
