The primary function of the Pascal Triangle Calculator is to provide immediate access to the values within Pascal’s Triangle at any row and position. It eliminates the need for manual calculations, thereby saving time and reducing potential errors. This is particularly beneficial in fields such as combinatorics, where such calculations are frequent.
Anyone dealing with mathematical computations can benefit from this calculator. It is especially useful for:
- Students learning combinatorics or probability
- Teachers preparing classroom materials
- Researchers conducting complex mathematical analyses
Formula of Pascal Triangle Calculator
At the heart of the calculator is the formula:
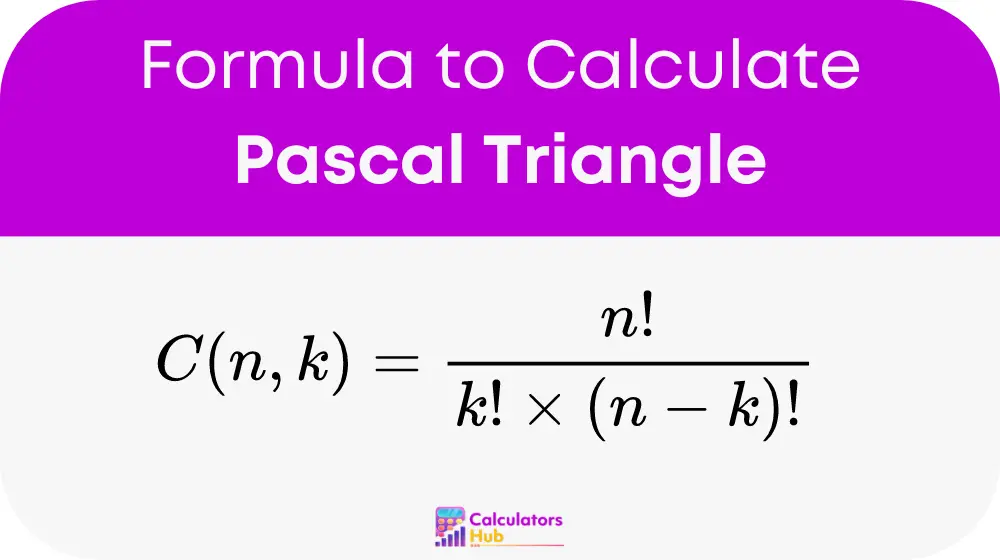
Component Explanation:
C(n, k): Known as the binomial coefficient, it represents the number of combinations of n items taken k at a time without regard to the order.n!: The factorial of n, the product of all positive integers up to n.k!: The factorial of k.(n - k)!: The factorial of (n – k).
Table for General Terms
To enhance usability, below is a quick reference table for Pascal’s Triangle:
| n (Row) | k (Position) | Value |
|---|---|---|
| 4 | 2 | 6 |
| 5 | 3 | 10 |
| 6 | 3 | 20 |
Using the Table: This table serves as a handy reference to quickly locate values without using the calculator, ideal for common calculations and enhancing problem-solving efficiency.
Example of Pascal Triangle Calculator
Calculation Process: Let’s calculate the value at the 5th row and 3rd position using the calculator:
- Select n = 5 (row) and k = 3 (position).
- Input these values into the calculator.
- The output will be
10, which is the binomial coefficientC(5, 3).
Visual Aids: (Insert diagram or screenshot of the calculator in use)
Most Common FAQs
Pascal’s Triangle is arranged such that each number is the sum of the two directly above it. Starting with 1 at the top, each row builds upon the previous ones to form a triangle of coefficients.
Reading the triangle is straightforward: each row corresponds to the powers of 11 (mathematically intriguing but practically limited view), and the positions correspond to the coefficients in the expansion of binomials.
Absolutely! The triangle is fundamental in calculating probabilities, especially in scenarios involving binomial expansions.
The calculator is designed to deliver highly accurate results, essential for academic and professional applications, ensuring reliability in critical mathematical calculations.