The Bowtie Angle Calculator is a useful tool designed to help individuals determine the angle formed by a bowtie shape. This calculator can be applied in various contexts, such as fashion design, geometry, or even in industrial applications where a bowtie shape is used for specific designs or functions. By using the width and height of the bowtie, the calculator provides an easy way to understand the angle created by the bowtie’s structure.
Bowties have a unique shape that can be challenging to measure manually, particularly when it comes to understanding the angle they form. The Bowtie Angle Calculator simplifies this task by using a straightforward mathematical formula, making it easier to measure and assess bowties for different purposes.
Formula of Bowtie Angle Calculator
The formula used to calculate the bowtie angle is:
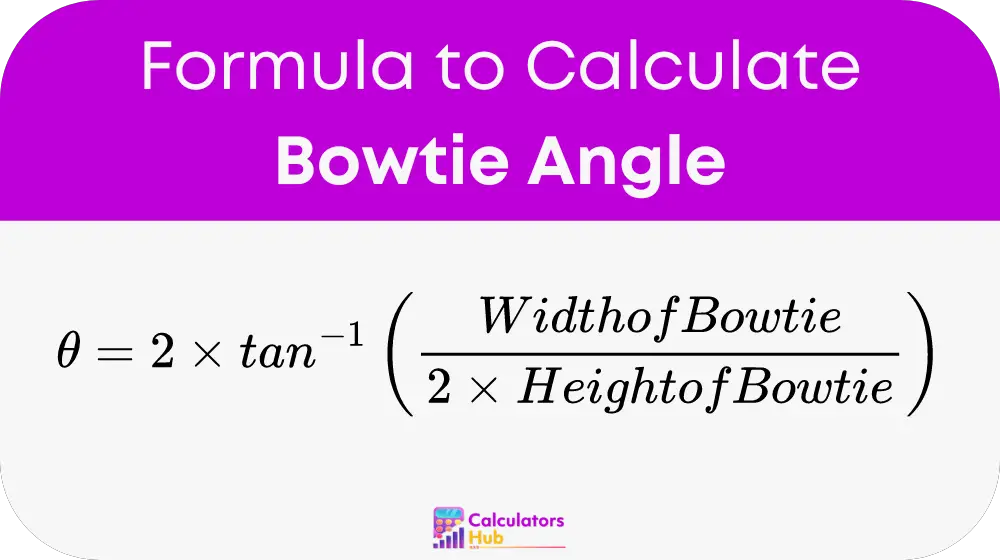
Variables:
- θ: Bowtie angle, measured in degrees, representing the angle formed by the bowtie.
- W: Width of the bowtie at its widest point, measured in centimeters or inches.
- H: Height of the bowtie from its center to the top or bottom edge, also measured in centimeters or inches.
Key Points:
- The width (W) of the bowtie refers to the measurement from one side of the bowtie to the other at its broadest part. This is important for understanding the overall spread of the bowtie.
- The height (H) refers to the vertical measurement from the center of the bowtie to either the top or the bottom edge. It helps determine the symmetry and proportions of the bowtie.
- The Bowtie Angle (θ) gives insight into the geometry of the bowtie shape, helping designers or tailors understand how the shape will look or function in a given context.
Common Terms and Reference Table
To help users better understand the Bowtie Angle Calculator and its components, here is a table of related terms and their meanings:
| Term | Definition |
|---|---|
| Bowtie Angle (θ) | The angle formed by the bowtie, measured in degrees. |
| Width (W) | The widest horizontal measurement of the bowtie, from side to side. |
| Height (H) | The vertical measurement of the bowtie, from the center to the edge. |
| Tan⁻¹ (Inverse Tangent) | A trigonometric function used to calculate the angle based on width and height proportions. |
| Degrees (°) | A unit for measuring angles. |
Example of Bowtie Angle Calculator
Let’s go through an example to illustrate how the Bowtie Angle Calculator works. Suppose we have a bowtie with the following measurements:
- Width (W): 12 centimeters
- Height (H): 6 centimeters
Step 1: Apply the Formula
Bowtie Angle (θ) = 2 × tan⁻¹((Width of Bowtie (W)) ÷ (2 × Height of Bowtie (H)))
Substitute the values:
θ = 2 × tan⁻¹((12) ÷ (2 × 6))
Step 2: Calculate
First, calculate the denominator:
2 × 6 = 12
Now divide the width by the result:
12 ÷ 12 = 1
Now, find the inverse tangent of 1:
tan⁻¹(1) = 45 degrees
Finally, multiply by 2:
θ = 2 × 45
θ = 90 degrees
In this case, the bowtie angle is 90 degrees, meaning the bowtie forms a right angle at its center.
Most Common FAQs
Calculating the bowtie angle is important in both design and functional applications. For fashion designers, it helps ensure that bowties have the correct proportions for aesthetics. In industrial or geometric contexts, knowing the angle can be crucial for ensuring the accuracy of designs that use the bowtie shape.
Yes, the Bowtie Angle Calculator can be applied to any object or design that follows a bowtie shape. It is not limited to fashion and can be used in architectural designs, graphics, or any geometric study involving this shape.
The width and height directly affect the bowtie angle because the angle is calculated based on their proportions. A wider bowtie with a shorter height will result in a smaller angle, while a taller bowtie with a narrower width will create a larger angle.