The Absolute Value of a Complex Number Calculator helps you find the distance of a complex number from the origin in the complex plane. This distance is also called the modulus or absolute value of the complex number. Knowing the absolute value is important in many mathematical and engineering applications because it shows the magnitude of complex numbers.
Formula
The absolute value (or modulus) of a complex number is a measure of its distance from the origin in the complex plane. Given a complex number z = a + bi, where a and b are real numbers, the formula for calculating the absolute value of z is:
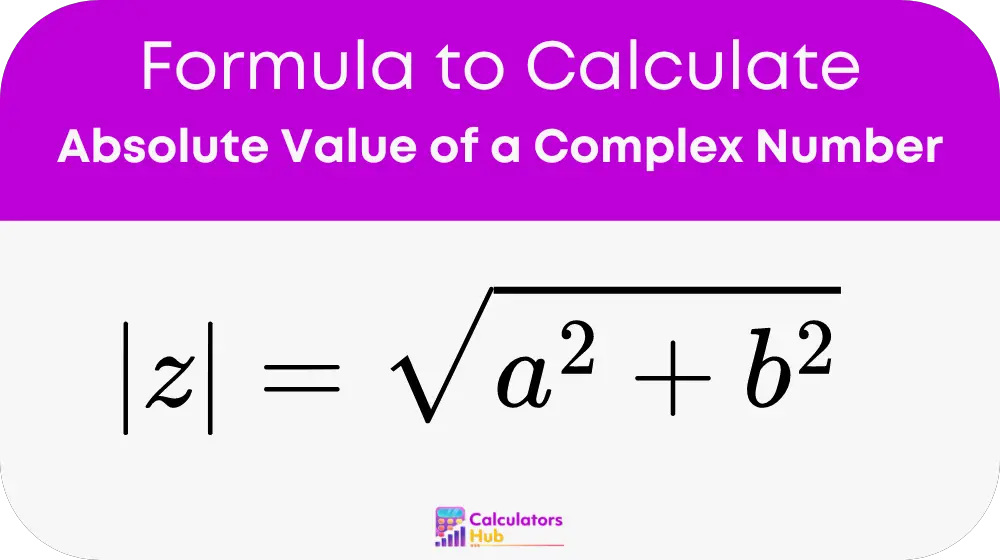
Here:
- a is the real part of the complex number.
- b is the imaginary part of the complex number.
- |z| represents the absolute value of the complex number.
- The square root function is denoted by sqrt().
Steps to Calculate the Absolute Value of a Complex Number:
- Identify the Real and Imaginary Parts: Determine the values of a (the real part) and b (the imaginary part) of the complex number z.
- Square the Real and Imaginary Parts: Calculate a^2 and b^2.
- Sum the Squares: Add the results from the previous step: a^2 + b^2.
- Compute the Square Root: Take the square root of the sum to find the absolute value.
Table for Common Terms and Conversions
Here is a table with some common complex numbers and their absolute values for quick reference:
| Complex Number | Absolute Value |
|---|---|
| 1 + 1i | 1.414 |
| 2 + 2i | 2.828 |
| 3 + 4i | 5 |
| 5 + 12i | 13 |
| 7 + 24i | 25 |
Example
Let’s consider a complex number z = 3 + 4i.
- Identify the Real and Imaginary Parts: a = 3, b = 4.
- Square the Real and Imaginary Parts: 3^2 = 9, 4^2 = 16.
- Sum the Squares: 9 + 16 = 25.
- Compute the Square Root: sqrt(25) = 5.
So, the absolute value of 3 + 4i is 5.
Most Common FAQs
A complex number is a number that has both a real part and an imaginary part. It is written in the form a + bi, where a is the real part and b is the imaginary part.
The absolute value of a complex number shows the distance from the origin in the complex plane. It is important in many fields such as engineering, physics, and applied mathematics.
The real part of a complex number is just one component of the number, while the absolute value takes into account both the real and imaginary parts to measure the overall magnitude of the complex number.