A Capacitor Discharge Calculator helps you determine how long it will take for a capacitor to discharge to a specific voltage in an RC (resistor-capacitor) circuit. Capacitors store electrical energy, but when disconnected from a power source, they discharge gradually over time, releasing their stored energy through a resistor. The rate at which this happens depends on both the resistance (R) and the capacitance (C) in the circuit.
In many electronics applications, understanding the discharge time is essential, especially in circuits involving timing, power management, or signal processing. The Capacitor Discharge Calculator simplifies this task by allowing you to input the initial voltage, resistance, and capacitance, and then it calculates the voltage across the capacitor at a given point in time during the discharge process.
Formula of Capacitor Discharge Calculator
The discharge of a capacitor is governed by an exponential decay function. The formula to calculate the voltage across a discharging capacitor is:
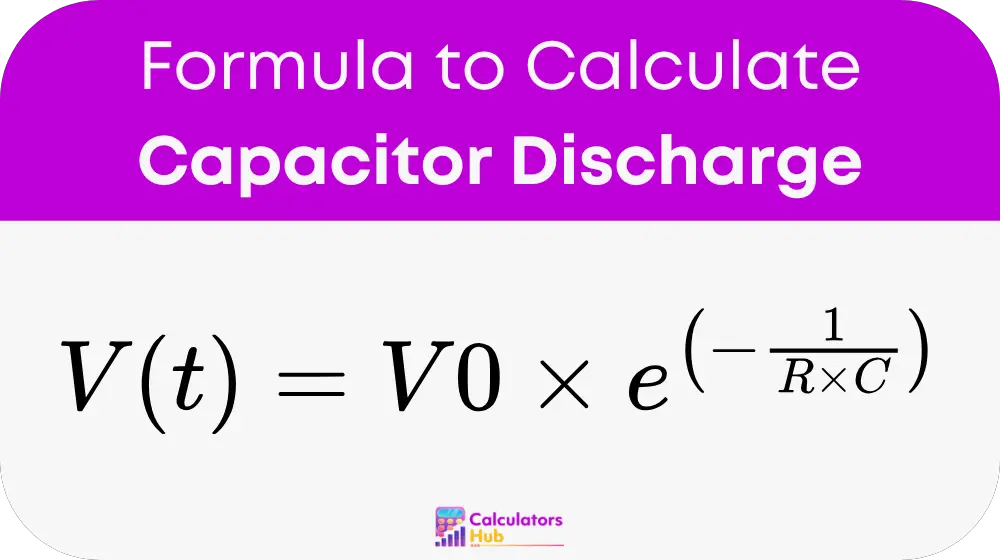
Where:
- V(t) = Voltage across the capacitor at time t in volts
- V0 = Initial voltage across the capacitor in volts
- t = Time in seconds
- R = Resistance in ohms
- C = Capacitance in farads
- e = Euler's number, approximately 2.718
This formula shows how the voltage across the capacitor decreases exponentially over time. The capacitor's voltage reduces more rapidly at first and slows down as it approaches zero, but it never reaches zero completely in theoretical terms.
Key Considerations
- Time Constant (τ): The time constant, denoted by τ = R * C, is the key factor in determining how quickly a capacitor discharges. After one time constant, the capacitor voltage decreases to about 36.8% of its initial value.
- Discharge Process: After 5 time constants (5 * R * C), the capacitor is considered fully discharged, meaning the voltage has decreased to less than 1% of its initial value.
General Capacitor Discharge Times
The table below provides a general understanding of how capacitor discharge works relative to the number of time constants that have passed. It demonstrates how quickly the voltage drops as the capacitor discharges.
| Time Constants (τ) | Voltage Across Capacitor (% of V0) | Description of Discharge Status |
|---|---|---|
| 1 τ (R * C) | 36.8% | Rapid initial discharge. |
| 2 τ | 13.5% | The rate of discharge slows. |
| 3 τ | 5.0% | Nearly fully discharged. |
| 4 τ | 1.8% | Approaching zero. |
| 5 τ | 0.7% | Essentially fully discharged. |
This table can help you estimate the discharge process based on the time constant without manually calculating each point in the curve. However, for more precise values, the Capacitor Discharge Calculator is a more efficient tool.
Example of Capacitor Discharge Calculator
Let’s consider a practical example of a capacitor discharging over time.
Example:
- Initial voltage (V0) = 10V
- Resistance (R) = 5kΩ (5,000 ohms)
- Capacitance (C) = 200µF (200 x 10^-6 farads)
- First, calculate the time constant τ:τ = R * C = 5,000 Ω * 200 x 10^-6 F = 1 second
- To find the voltage after 3 seconds of discharge, we plug the values into the formula:V(3) = 10V * e^(-3 / 1)Using Euler’s number e ≈ 2.718, we get:V(3) ≈ 10V * e^(-3) ≈ 10V * 0.0498 ≈ 0.498V
So, after 3 seconds, the capacitor has discharged to approximately 0.498 volts. This shows how quickly the capacitor discharges, and how the voltage approaches zero over time.
Most Common FAQs
A capacitor is considered fully discharged after 5 time constants (5 * R * C). At this point, the voltage across the capacitor has dropped to less than 1% of its initial value.
The discharge time depends on the resistance (R) and capacitance (C) in the circuit. A higher resistance or capacitance will increase the discharge time, while lower values will decrease it.
Increasing the resistance or capacitance will increase the time constant (τ = R * C), making the discharge process slower. Conversely, reducing either the resistance or capacitance will result in a faster discharge.