The Absolute Age Calculator calculates the age of geological samples using radiometric dating techniques. It measures the decay of radioactive isotopes within the sample, providing an accurate age based on the known half-lives of these isotopes. This information is important for understanding the formation and history of rocks, fossils, and other geological materials.
Formula of Absolute Age Calculator
Absolute age is determined using radiometric dating methods. The formula for calculating absolute age involves:
- Half-life: The time it takes for half of a given amount of a radioactive isotope to decay.
- Parent isotope: The original radioactive isotope.
- Daughter isotope: The product of the decay of the parent isotope.
The formula for calculating the absolute age is:
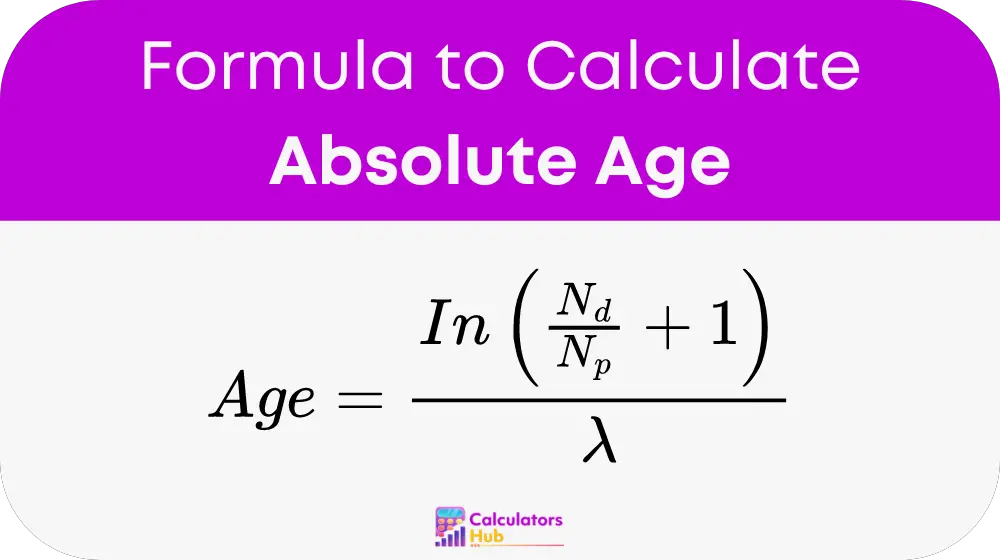
Where:
- Nd is the number of daughter isotopes.
- Np is the number of remaining parent isotopes.
- λ is the decay constant, related to the half-life (t1/2) by the formula λ = ln(2) / t1/2.
Explanation of Terms:
- Nd (Number of Daughter Isotopes): This represents the quantity of isotopes that have resulted from the decay of the parent isotope.
- Np (Number of Parent Isotopes): This indicates the remaining quantity of the original radioactive isotope.
- λ (Decay Constant): This is a value that describes the rate of decay of the radioactive isotope, calculated from its half-life.
Pre-Calculated Table for Common Searches
Below is a table with pre-calculated values for commonly searched isotopes and their respective ages. This helps users to quickly find the age without performing calculations each time.
| Parent Isotope | Daughter Isotope | Half-Life (Years) | Age (Years) |
|---|---|---|---|
| Uranium-238 | Lead-206 | 4.5 billion | 4.5 billion |
| Carbon-14 | Nitrogen-14 | 5,730 | 5,730 |
| Potassium-40 | Argon-40 | 1.3 billion | 1.3 billion |
Example of Absolute Age Calculator
Let’s consider an example to show how to use the Absolute Age Calculator. Suppose we have a rock sample containing 1000 parent isotopes (Uranium-238) and 3000 daughter isotopes (Lead-206). The half-life of Uranium-238 is approximately 4.5 billion years.
Using the formula:
Age = ln((3000 / 1000) + 1) / 1.54 x 10^-10 ≈ 4.5 billion years
This calculation shows that the rock sample is approximately 4.5 billion years old.
Most Common FAQs
Absolute age dating provides precise age measurements, which are important for understanding the timing and sequence of geological events. It helps scientists reconstruct the history of the Earth and study the age of various materials.
The accuracy of the Absolute Age Calculator depends on the precision of the input data and the reliability of the half-life values used. Generally, radiometric dating methods are highly accurate when proper techniques and calibrations are applied.
The Absolute Age Calculator can be use for rocks containing suitable parent and daughter isotopes. It is commonly use for igneous and metamorphic rocks but may not be applicable to sedimentary rocks unless they contain specific minerals suitable for dating.