The Slant Height of a Cone Calculator helps you find the slant height of a cone easily. The slant height is the distance from the base of the cone to its top along the surface of the cone. This tool makes it simple to get this measurement without doing the math by hand.
Formula of Slant Height of a Cone Calculator
To calculate the slant height, use this formula:
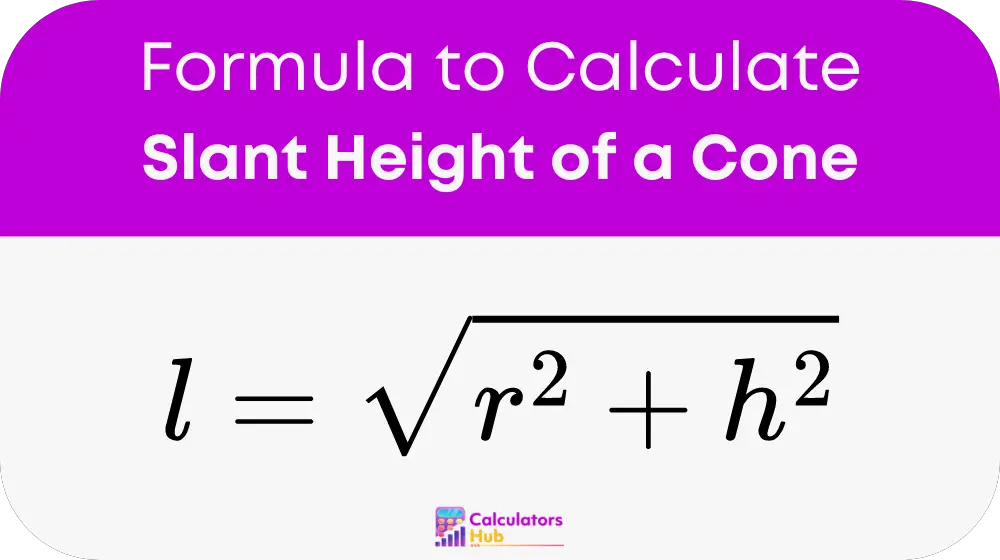
Where:
- l is the slant height
- r is the radius of the base of the cone
- h is the height of the cone
This formula comes from the Pythagorean theorem, which applies to the right triangle formed by the radius, height, and slant height of the cone.
Pre-calculated Slant Heights Table
Here is a table with some common values for radius and height, and their corresponding slant heights:
| Radius (r) | Height (h) | Slant Height (l) |
|---|---|---|
| 1 | 1 | 1.41 |
| 2 | 2 | 2.83 |
| 3 | 4 | 5 |
| 4 | 6 | 7.21 |
| 5 | 8 | 9.43 |
This table allows you to quickly find the slant height without calculating each time.
Example of Slant Height of a Cone Calculator
Let's look at an example to see how the calculator works.
If a cone has a radius of 3 units and a height of 4 units, follow these steps to find the slant height:
- Square the radius: 3^2 = 9
- Square the height: 4^2 = 16
- Add the squared values: 9 + 16 = 25
- Take the square root of the sum: sqrt(25) = 5
So, the slant height (l) is 5 units.
Most Common FAQs
The calculator is very accurate as it uses the exact mathematical formula. The accuracy depends on how precise your input values are.
Yes, the calculator can work with decimal values for both the radius and the height, which is useful for more precise measurements.
Knowing the slant height is important for many tasks, such as calculating the surface area of a cone, designing objects like funnels and lampshades, and in construction projects involving conical shapes.