A Fraction Exponent Calculator is a mathematical tool designed to raise a fraction to any given power, also known as an exponent. This operation involves applying the exponent to both the top part (numerator) and the bottom part (denominator) of the fraction separately. This calculator is particularly useful for students learning algebra, as it helps clarify the rules of exponents with fractions. It is also a valuable resource in various scientific and engineering fields where such calculations are common. Consequently, this tool simplifies a potentially complex calculation into a straightforward process, providing an accurate and simplified result.
formula of Fraction Exponent Calculator
To raise a fraction to a power, you apply the exponent to both the numerator and the denominator individually.
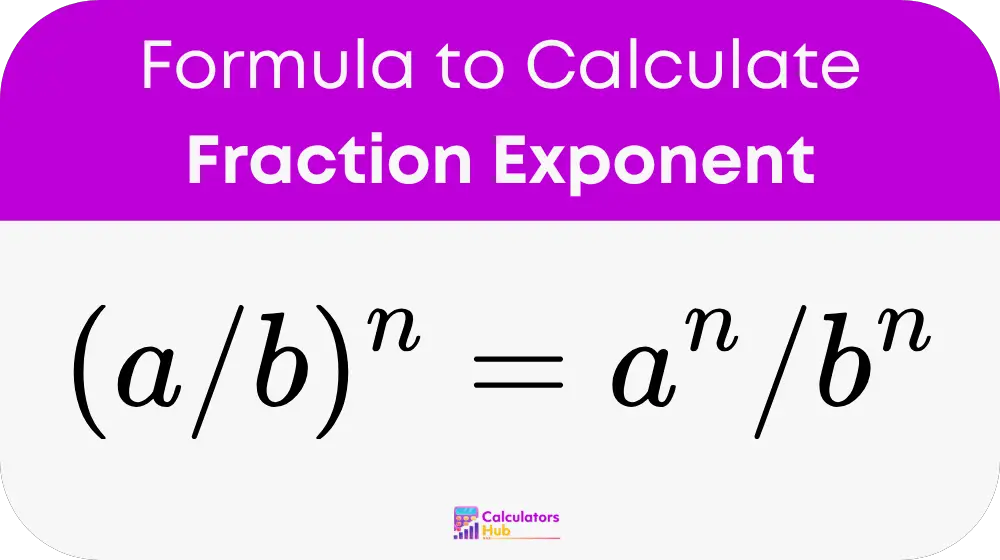
Where:
- a/b is the base fraction.
- n is the exponent (this can be a positive or negative whole number, or even a fraction itself).
- a^n means the numerator ‘a’ is raised to the power of ‘n’.
- b^n means the denominator ‘b’ is raised to the power of ‘n’.
Common Fractions Raised to Powers
This table provides a quick reference for the results of common fractions raised to simple integer powers. This helps in visualizing the effect of exponents on fractions.
| Base Fraction (a/b) | Exponent (n) | Result (a^n / b^n) |
| 1/2 | 2 | 1/4 |
| 1/2 | 3 | 1/8 |
| 1/3 | 2 | 1/9 |
| 1/3 | 3 | 1/27 |
| 2/3 | 2 | 4/9 |
| 2/3 | 3 | 8/27 |
| 3/4 | 2 | 9/16 |
| 3/4 | 3 | 27/64 |
Example of Fraction Exponent Calculator
Let’s calculate the value of the fraction (2/5) raised to the power of 3.
Step 1: Identify the base fraction and the exponent.
- Base Fraction: 2/5
- Exponent: 3
Step 2: Apply the exponent to the numerator.
Numerator = 2^3 = 2 × 2 × 2 = 8
Step 3: Apply the exponent to the denominator.
Denominator = 5^3 = 5 × 5 × 5 = 125
Step 4: Combine the new numerator and denominator to form the final fraction.
The result is 8/125.
Since 8 and 125 do not share any common factors, the fraction is already in its simplest form. Therefore, (2/5)^3 = 8/125.
Most Common FAQs
A negative exponent means you should first take the reciprocal of the base fraction (flip it upside down) and then apply the positive version of the exponent. For example, to solve (2/3)^-2, you would first flip 2/3 to get 3/2, and then calculate (3/2)^2, which equals 9/4.
A fractional exponent indicates a root. An exponent of 1/2 is the same as taking the square root, and an exponent of 1/3 is the same as taking the cube root. You apply the root to both the numerator and the denominator. For example, (9/16)^(1/2) is the same as √9 / √16, which equals 3/4.
According to the rules of exponents, any non-zero number or fraction raised to the power of zero is always equal to 1. For example, (3/5)^0 = 1.