A Decay Percentage Calculator helps scientists, engineers, and analysts determine how much of a substance, investment, or value has decayed over a given time. It is widely used in nuclear physics, chemistry, finance, and environmental sciences to measure how quickly a quantity diminishes based on its half-life and the elapsed time.
This calculator is particularly useful for radioactive decay calculations, investment depreciation, and signal processing where values gradually decrease over time. By computing the decay percentage, users can quantify the reduction in a material’s activity, a financial asset’s value, or any process that follows exponential decay.
Formula for Decay Percentage Calculator
The Decay Percentage is calculated using the exponential decay equation:
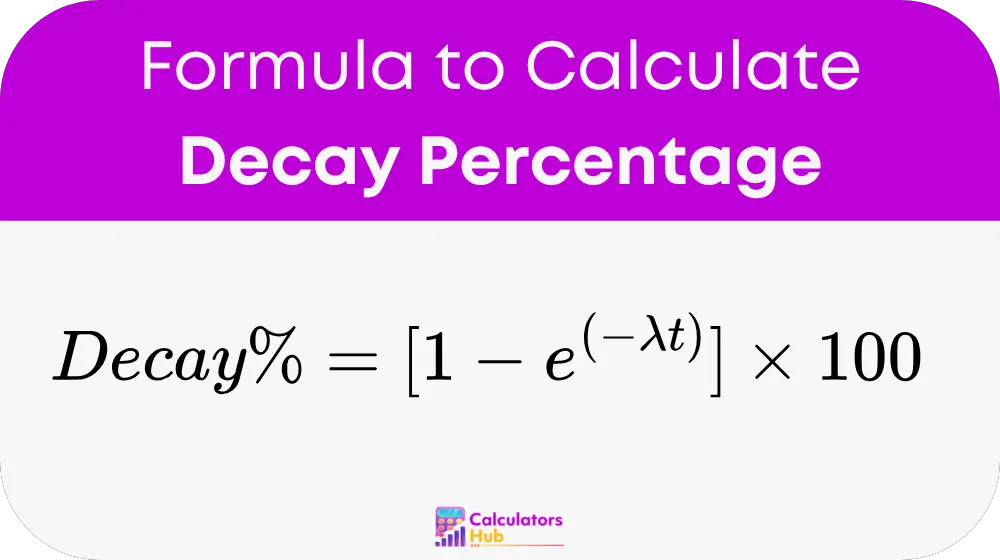
Where:
λ (Decay Constant) = ln(2) ÷ Half-life
t = Time elapsed
e = Euler’s number (≈ 2.718)
This formula helps determine the percentage of the original value lost after a specific time, providing a precise way to track decay rates across different applications.
Decay Percentage Reference Table
To simplify decay calculations, the following table provides estimated decay percentages for different half-lives and time values.
| Half-life (Hours) | Time Elapsed (Hours) | Decay Constant (λ) | Decay Percentage (%) |
|---|---|---|---|
| 1 | 1 | 0.693 | 50.0 |
| 3 | 3 | 0.231 | 50.0 |
| 6 | 6 | 0.116 | 50.0 |
| 10 | 5 | 0.069 | 39.5 |
| 24 | 12 | 0.029 | 26.1 |
This table allows users to estimate decay percentage values without manual calculations, making it valuable in radiation decay analysis, chemical reactions, and financial depreciation tracking.
Example of Decay Percentage Calculator
A scientist is analyzing a radioactive isotope with a half-life of 8 hours, and they want to calculate the decay percentage after 16 hours.
Step 1: Calculate the Decay Constant
λ = ln(2) ÷ Half-life
λ = 0.693 ÷ 8 ≈ 0.0866 per hour
Step 2: Apply the Decay Percentage Formula
Decay Percentage = [1 - e^(-0.0866 × 16)] × 100
Step 3: Compute the Result
Decay Percentage ≈ 75.0%
After 16 hours, 75% of the material has decayed, leaving only 25% of the original substance.
Most Common FAQs
The decay percentage quantifies how much of a substance or value has diminished over a certain period. It is widely use in physics, chemistry, and finance to measure how quickly a quantity loses its value over time.
The half-life determines the rate of decay. A shorter half-life results in faster decay, meaning a higher percentage loss over a shorter time. A longer half-life leads to slower decay, preserving more of the original material for a longer duration.
Yes, decay percentage is use in financial modeling, signal processing, and medical research. It helps analyze how assets depreciate over time, how signals fade in communication systems, and how biological substances break down in the human body.