The Coil (Conical) Spring Force Calculator is a tool that computes the force exerted by a conical spring under compression or extension. Conical springs, also known as tapered springs, have variable diameters, allowing for a compact design and nonlinear load-bearing capabilities. These springs are widely used in mechanical systems where space constraints and controlled force are important. The calculator simplifies the process of determining the force by accounting for essential parameters like the spring constant, material properties, and deformation. It belongs to the category of mechanical design tools, aiding engineers and designers in accurately analyzing spring behavior.
Formula of Coil (Conical) Spring Force Calculator
The force exerted by a conical coil spring is calculated using the formula:
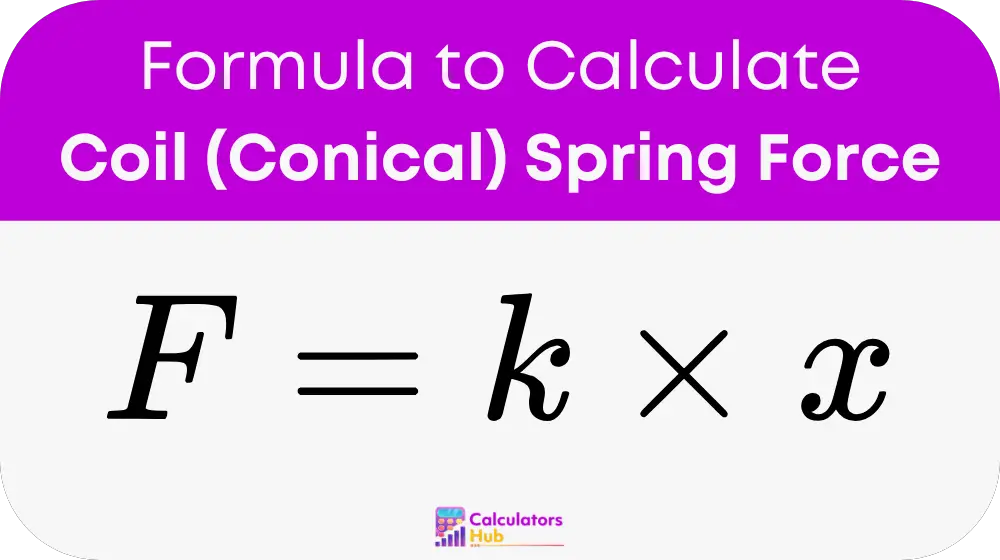
Where:
- F is the force exerted by the spring (Newtons).
- k is the spring constant (N/m).
- x is the compression or extension of the spring (meters).
Detailed Calculation for the Spring Constant (k):
The spring constant is derived from the material properties and geometric characteristics of the spring:
k = (G * d^4) / (8 * N * R_mean^3)
Where:
- G is the modulus of rigidity of the spring material (N/m²).
- d is the wire diameter (meters).
- N is the total number of active coils.
- R_mean is the average radius of the coils (meters).
Calculation of the Average Radius (R_mean):
The average radius is calculated as:
R_mean = (R_top + R_base) / 2
Where:
- R_top is the radius of the smallest coil at the top of the conical spring (meters).
- R_base is the radius of the largest coil at the base of the conical spring (meters).
Pre-Calculated Table for Common Conical Spring Parameters
Here is a reference table for typical conical spring parameters and their resulting spring constants for common materials:
| Material | Wire Diameter (d) | Number of Coils (N) | Average Radius (R_mean) | Modulus of Rigidity (G) | Spring Constant (k) |
|---|---|---|---|---|---|
| Steel | 0.005 m | 10 | 0.02 m | 79 × 10⁹ N/m² | 98 N/m |
| Stainless Steel | 0.006 m | 8 | 0.025 m | 77 × 10⁹ N/m² | 132 N/m |
| Copper | 0.004 m | 12 | 0.015 m | 44 × 10⁹ N/m² | 68 N/m |
| Aluminum Alloy | 0.007 m | 6 | 0.03 m | 26 × 10⁹ N/m² | 44 N/m |
This table helps in quick estimations and is particularly useful for preliminary design.
Example of Coil (Conical) Spring Force Calculator
Let’s calculate the force exerted by a conical spring with the following parameters:
- Wire diameter (d) = 0.005 m.
- Number of active coils (N) = 10.
- Radius of the smallest coil (R_top) = 0.015 m.
- Radius of the largest coil (R_base) = 0.025 m.
- Modulus of rigidity (G) = 79 × 10⁹ N/m².
- Compression (x) = 0.01 m.
Step 1: Calculate the Average Radius
R_mean = (R_top + R_base) / 2
R_mean = (0.015 + 0.025) / 2 = 0.02 m
Step 2: Calculate the Spring Constant
k = (G * d^4) / (8 * N * R_mean^3)
k = (79 × 10⁹ * (0.005)^4) / (8 × 10 × (0.02)^3) ≈ 98 N/m
Step 3: Calculate the Force
F = k * x
F = 98 × 0.01 = 0.98 N
Thus, the spring exerts a force of 0.98 Newtons under the given compression.
Most Common FAQs
Conical springs provide a compact design with variable stiffness, allowing for better load management and space-saving applications.
The modulus of rigidity is a material property obtain from engineering handbooks or manufacturer specifications. It represents the material’s resistance to shear deformation.
Yes, the same principles apply, but the deformation (x) will represent extension rather than compression.