The Blackbody Energy Calculator is a tool used to determine the amount of energy radiated per unit area by a blackbody. A blackbody is an idealized physical object that absorbs all incident radiation and re-emits energy as thermal radiation. This calculator applies the Stefan-Boltzmann Law to compute the total energy radiated by a blackbody at a given temperature.
Formula of Blackbody Energy Calculator
To calculate the energy radiated per unit area, use the following formula:
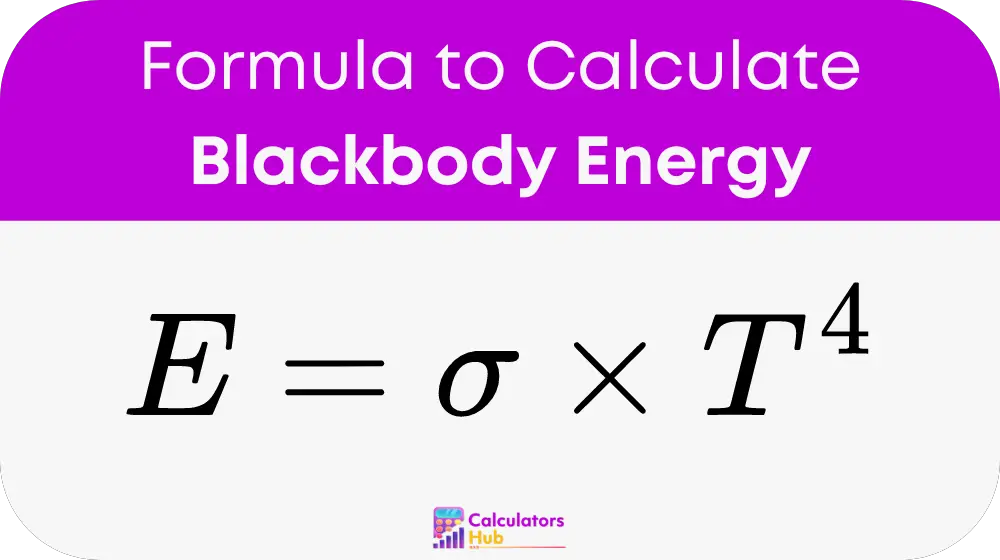
Where:
- E = Energy radiated per unit area (W/m²)
- σ = Stefan-Boltzmann constant, approximately 5.670374419 × 10^-8 W/m²K⁴
- T = Absolute temperature of the blackbody in Kelvin (K)
General Reference Table
For convenience, here is a table showing the energy radiated per unit area at various temperatures:
| Temperature (K) | Energy Radiated per Unit Area (W/m²) |
|---|---|
| 300 | 2.77 × 10^4 |
| 400 | 5.11 × 10^4 |
| 500 | 8.13 × 10^4 |
| 600 | 1.17 × 10^5 |
| 700 | 1.56 × 10^5 |
| 800 | 2.00 × 10^5 |
Example of Blackbody Energy Calculator
If the temperature of the blackbody is 600 K, the energy radiated per unit area can be calculated as follows:
- T = 600 K
- σ = 5.670374419 × 10^-8 W/m²K⁴
Apply the Formula:
E = 5.670374419 × 10^-8 * (600)^4
E ≈ 5.670374419 × 10^-8 * 1.296 × 10^8
≈ 7.36 × 10^1 W/m²
Thus, the energy radiated per unit area is approximately 73.6 W/m².
Most Common FAQs
A blackbody is an idealized object that absorbs all incoming radiation and re-emits energy as thermal radiation. It is used in theoretical physics to study radiation and energy transfer.
The energy radiated by a blackbody increases with the fourth power of its temperature. This means that even small increases in temperature result in large increases in the amount of energy radiated.
The calculator specifically applies to ideal blackbodies. For real objects, which are not perfect blackbodies, emissivity factors must be consider to accurately determine energy radiated.