The Axial Force Calculator is designed to calculate the force applied along the axis of a cylindrical or prismatic object. This calculation is crucial in many engineering fields as it helps determine the load that an object can withstand before failing. It's particularly useful in the design and analysis of columns, struts, and other structural elements that are subject to axial loading.
Formula of Axial Force Calculator
To accurately compute axial force, the following detailed formula is employed:
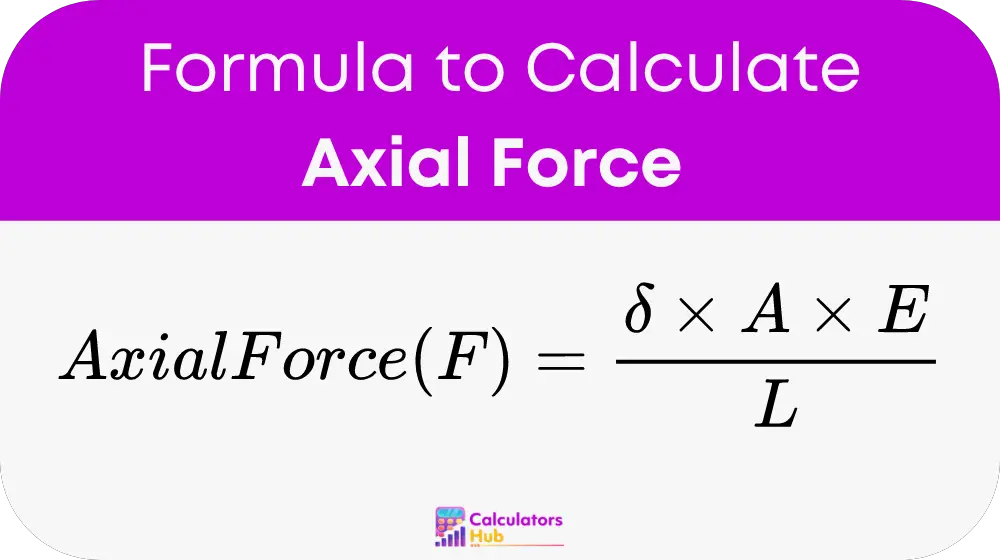
Where:
- Axial Force (F): The force applied along the axis of the object.
- Axial Deformation (δ): The change in length due to the applied force.
- Area (A): The cross-sectional area of the object.
- Modulus of Elasticity (E): The material's modulus of elasticity, a measure of a material's ability to deform elastically.
- Length (L): The original length of the object.
This formula allows for precise calculation of axial force by incorporating the object’s material properties, dimensions, and the extent of deformation experienced.
Table for General Terms
To aid in understanding and utilizing the Axial Force Calculator, here’s a table of common terms used in this context:
| Term | Definition |
|---|---|
| Axial Force (F) | The force applied along the axis of an object |
| Axial Deformation (δ) | The change in length of an object due to applied force |
| Area (A) | The cross-sectional area through which the force is applied |
| Modulus of Elasticity (E) | A measure of a material’s ability to deform elastically |
| Length (L) | The original length of the object |
Example of Axial Force Calculator
Consider a steel rod with a length of 2 meters, a cross-sectional area of 0.01 square meters, and a modulus of elasticity of 210 GPa (gigapascals). If the rod undergoes an axial deformation of 0.005 meters:
Axial Force (F) = (0.005 m * 0.01 m² * 210 GPa) / 2 m = 5.25 kN (kilonewtons)
This example demonstrates how the axial force calculator can be used to estimate the load capacity of structural components, ensuring they are designed to withstand specific loads.
Most Common FAQs
A1: Accurately calculating axial force is crucial for ensuring the structural integrity and safety of engineering projects. Incorrect calculations can lead to over- or under-designed structures, potentially causing structural failures.
A2: Axial force calculations are fundamental in designing beams, columns, and other load-bearing elements in buildings, bridges, and various structures. They are also use in mechanical engineering applications such as shafts and hydraulic cylinders.
A3: Material properties such as modulus of elasticity and yield strength are essential in determining how much load a material can support before deforming or failing. Different materials will react differently under the same load conditions, affecting the design and safety factors.