The Artillery Range Calculator is designed to compute the maximum horizontal distance (range) that an artillery projectile will travel when fired at a certain angle with a specific initial velocity. This tool is vital for military strategists and engineers to determine how to effectively deploy artillery units in combat or training exercises. It factors in variables such as muzzle velocity, projectile weight, air resistance, and the angle of launch to provide accurate and reliable results.
Formula of Artillery Range Calculator
The fundamental formula used by the Artillery Range Calculator is based on the principles of projectile motion in physics:
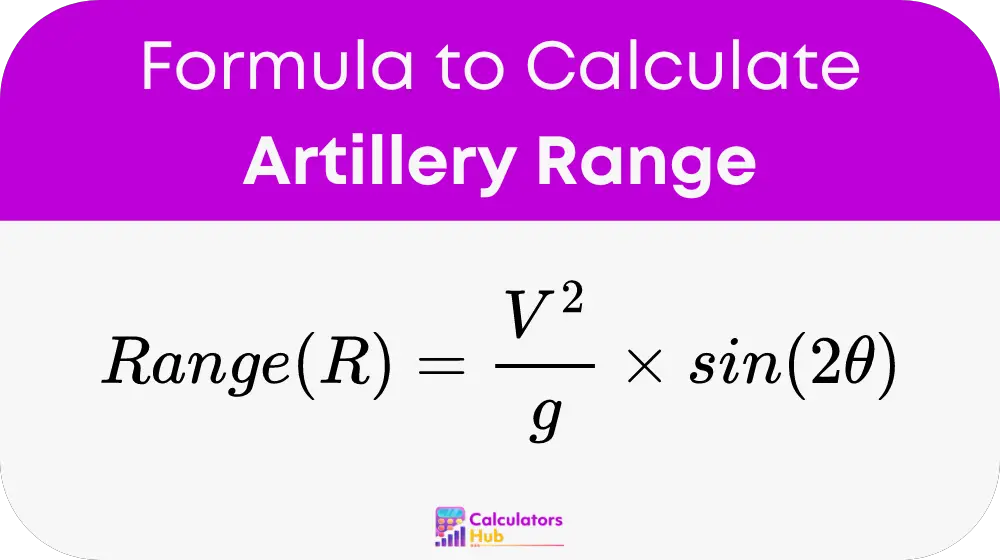
Where:
- Range (R) is the horizontal distance the projectile travels, measured in meters.
- V is the muzzle velocity of the projectile, measured in meters per second (m/s).
- g is the acceleration due to gravity, approximately 9.81 meters per second squared (m/s²).
- θ is the angle of elevation from the horizontal, measured in radians.
This formula captures the essence of how varying the launch angle and velocity impacts the distance a projectile can cover.
Table of General Terms
Here’s a table that defines key terms associated with the Artillery Range Calculator:
| Term | Definition | Example Values |
|---|---|---|
| Range (R) | The maximum horizontal distance a projectile travels | 2000 meters, 3000 meters |
| Muzzle Velocity (V) | Initial speed of the projectile as it leaves the barrel | 800 m/s, 1000 m/s |
| Acceleration due to Gravity (g) | Constant force acting on the projectile | 9.81 m/s² |
| Angle of Elevation (θ) | The angle at which the projectile is fired | 45 degrees (0.785 radians) |
Example of Artillery Range Calculator
For instance, if an artillery unit fires a projectile with a muzzle velocity of 500 m/s at an angle of 45 degrees (0.785 radians), the range can be calculated as:
R = (500² / 9.81) × sin(2 × 0.785) = 2550 meters
This calculation shows how the calculator determines the distance the projectile will travel, allowing for precise adjustments in real-world applications.
Most Common FAQs
A1: The basic formula provided does not account for air resistance; however, advanced versions of the calculator may include drag coefficients to provide more accurate estimations in real-world conditions.
A2: Yes, while design primarily for artillery, the calculator can theoretically be use for any projectile as long as the appropriate input values are provide.
A3: Yes, versions of this calculator are use in military operations to plan artillery deployment. It ensure the effective use of firepower.