This specialized calculator provides a swift and accurate method to determine the perimeter of a regular polygon when you know the radius of the inscribed circle. Regular polygons have all sides of equal length, and an inscribed circle (or "incircle") which is a circle perfectly containe within the vertexes of the polygon. The radius of this circle is a key component in calculating the perimeter.
Formula for Calculating the Perimeter
For regular polygons, the formula to calculate the perimeter (P) when the radius (r) of the inscribed circle is known is surprisingly straightforward:
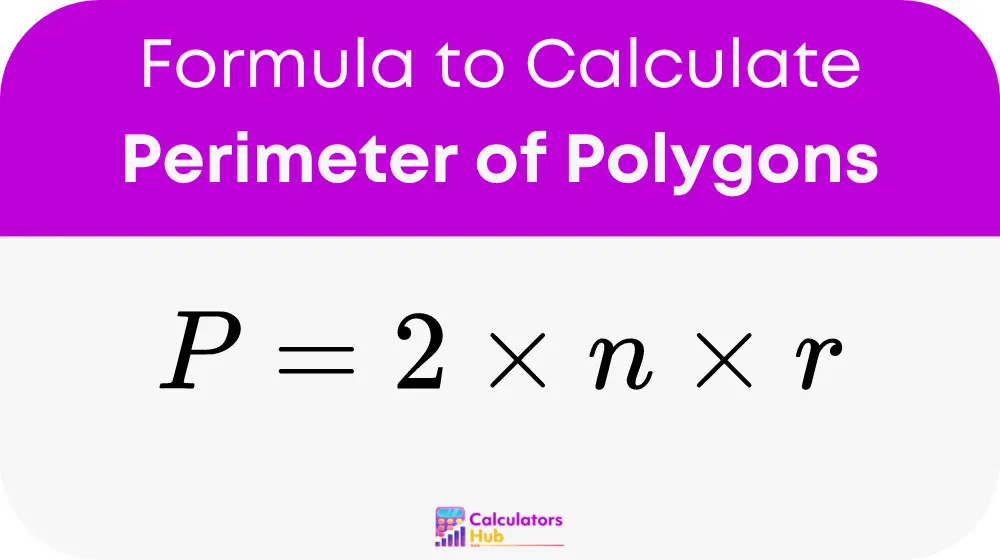
Where:
-
nis the number of sides of the polygon, -
ris the radius of the inscribed circle.
This formula works under the principle that the polygon can be divided into n identical isosceles triangles, each having a base angle of 360/n degrees and sides of length r (the radius). The perimeter is simply the sum of all side lengths of these triangles.
Table of Common Calculations
Number of Sides (n) |
Radius (r) |
Perimeter (P) |
|---|---|---|
| 3 | 1 cm | 6 cm |
| 4 | 1 cm | 8 cm |
| 5 | 1 cm | 10 cm |
| 6 | 1 cm | 12 cm |
| This table serves as a quick reference to understand how changes in the number of sides and radius affect the perimeter. |
Example Calculations
Example 1: Triangle with radius of 1 cm
For a triangle (3 sides) with an inscribed circle of radius 1 cm:
P = 2 * 3 * 1 = 6 c
Example 2: Square with radius of 1 cm
For a square (4 sides) with an inscribed circle of radius 1 cm:
P = 2 * 4 * 1 = 8 cm
Most Common FAQs
A1: A regular polygon is a polygon where all angles are equal and all sides are the same length.
A2: The radius of an inscribed circle can be found using the area of the polygon and the semiperimeter (half the perimeter) through the formula r = Area/Semiperimeter.
A3: No, this formula is specific to regular polygons due to their symmetrical nature.