The Latus Rectum of a Parabola Calculator is a specialized tool designed to calculate the length of the latus rectum of a parabola given specific coefficients of the parabolic equation. This tool simplifies the process, enabling both students and professionals to perform quick and accurate calculations without manual effort.
Formula of Latus Rectum of Parabola Calculator
The formula to calculate the latus rectum (LR) of a parabola is straightforward:
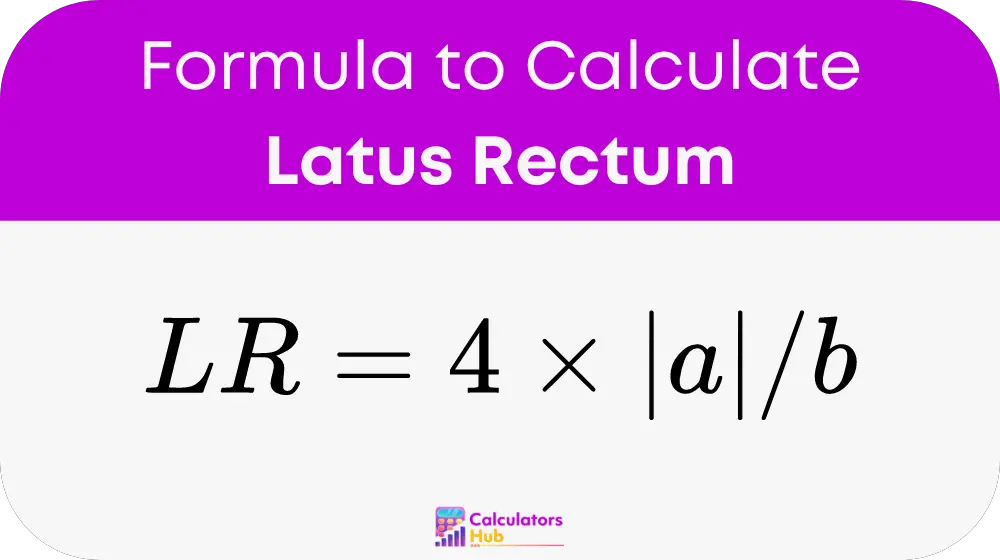
Here, LR represents the length of the latus rectum, |a| is the absolute value of the coefficient of the squared term (x^2), and b is the coefficient of the linear term (x) in the equation of the parabola y = ax^2 + bx + c. Understanding this formula is crucial for anyone studying the geometrical properties of parabolas.
Useful Reference Table
To further aid in understanding, here is a table with common values for a and b and the resulting latus rectum lengths:
| Coefficient a | Coefficient b | Latus Rectum LR |
|---|---|---|
| 1 | 2 | 2 |
| 1 | 3 | 1.33 |
| 2 | 2 | 4 |
This table serves as a quick reference for common calculations, assisting users in bypassing the need for manual calculations.
Example of Latus Rectum of Parabola Calculator
Consider the parabolic equation y = 2x^2 + 4x + 1. To find the latus rectum:
LR = 4 * |2| / 4 = 2
This calculation shows that the latus rectum of the parabola is 2 units long.
Most Common FAQs
The latus rectum is a line segment perpendicular to the axis of symmetry of the parabola, passing through its focus, and its length reflects key aspects of the parabola’s curvature.
You can calculate it using the formula LR = 4 * |a| / b, where a and b are coefficients from the standard parabolic equation.
Yes, this calculator works for any parabola, as long as you know the coefficients a and b from its equation.
