A Cosecant Calculator is a mathematical tool designed to compute the cosecant of a given angle. The cosecant function is the reciprocal of the sine function, making it an essential part of trigonometry. This calculator is especially useful in fields like engineering, physics, architecture, and mathematics where trigonometric calculations are frequently needed.
By inputting an angle in degrees or radians, the Cosecant Calculator provides the cosecant value with precision, saving time and eliminating manual calculations. It is particularly valuable when solving complex trigonometric equations or analyzing periodic phenomena.
Formula of Cosecant Calculator
The formula to calculate the cosecant of an angle is:
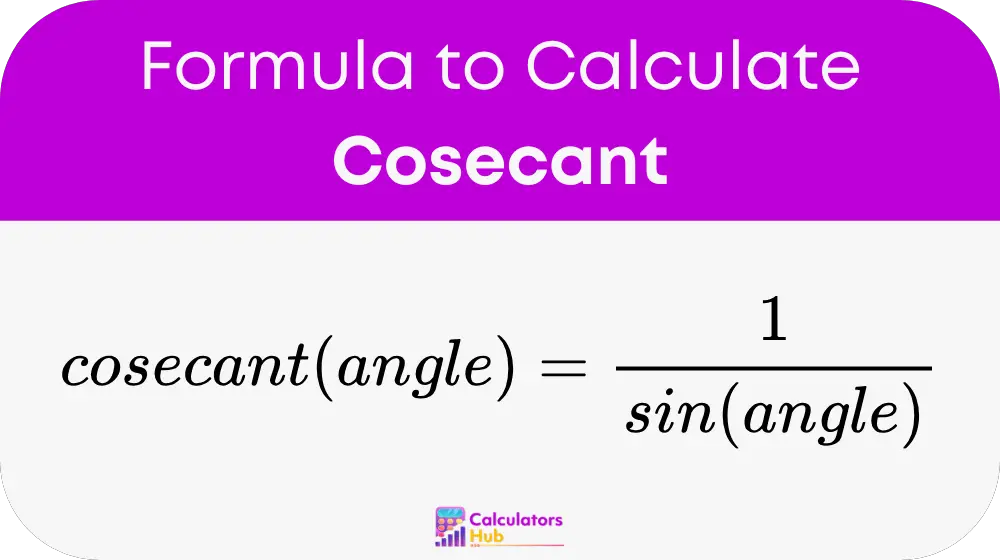
Detailed Formula Components
- Angle:
The input value, which can be expressed in degrees or radians, represents the angle for which the cosecant is being calculated. - sin(angle):
The sine of the given angle, which is a fundamental trigonometric ratio. The sine value can be obtained using a sine table, calculator, or trigonometric function. - cosecant(angle):
The reciprocal of the sine value. It represents the ratio of the hypotenuse to the opposite side in a right-angled triangle.
Note:
The sine of an angle must not be zero, as division by zero is undefined.
General Terms Table
The table below lists common angles and their cosecant values for quick reference:
| Angle (Degrees) | sin(angle) | cosecant(angle) |
|---|---|---|
| 30° | 0.5 | 2.0 |
| 45° | 0.7071 | 1.4142 |
| 60° | 0.8660 | 1.1547 |
| 90° | 1.0 | 1.0 |
| 120° | 0.8660 | 1.1547 |
| 180° | 0.0 (undefined) | Undefined |
This table allows users to quickly reference common angles without needing to perform calculations.
Example of Cosecant Calculator
Scenario:
A student needs to find the cosecant of a 45° angle.
Calculation:
Using the formula:
cosecant(angle) = 1 / sin(angle)
Substitute the sine value for 45° (approximately 0.7071):
cosecant(45°) = 1 / 0.7071
Result:
cosecant(45°) ≈ 1.4142
Interpretation:
The cosecant of a 45° angle is approximately 1.4142.
Most Common FAQs
The Cosecant Calculator is design to simplify trigonometric calculations by providing the cosecant value of an angle instantly. It eliminates manual computations and ensures accuracy.
Yes, the cosecant value is undefined when the sine of the angle is zero. This occurs at multiples of 180° (or π radians), such as 0°, 180°, 360°, and so on.
Cosecant has practical applications in physics, engineering, and architecture. It is often use to model wave patterns, design structures, and analyze periodic functions in various industries.