The 75 Chebyshev Interval Calculator helps users find the range within which 75 percent of data points in a distribution fall. This is based on Chebyshev's inequality, a fundamental theorem in probability theory. The calculator is especially useful in cases where the distribution is not normal, providing a reliable interval estimation regardless of the data's distribution shape.
Formula of 75 Chebyshev Interval Calculator
The Chebyshev interval calculator helps to determine the interval within which a certain percentage of data points lie in a distribution, based on Chebyshev's inequality.
Formula for the Chebyshev interval:
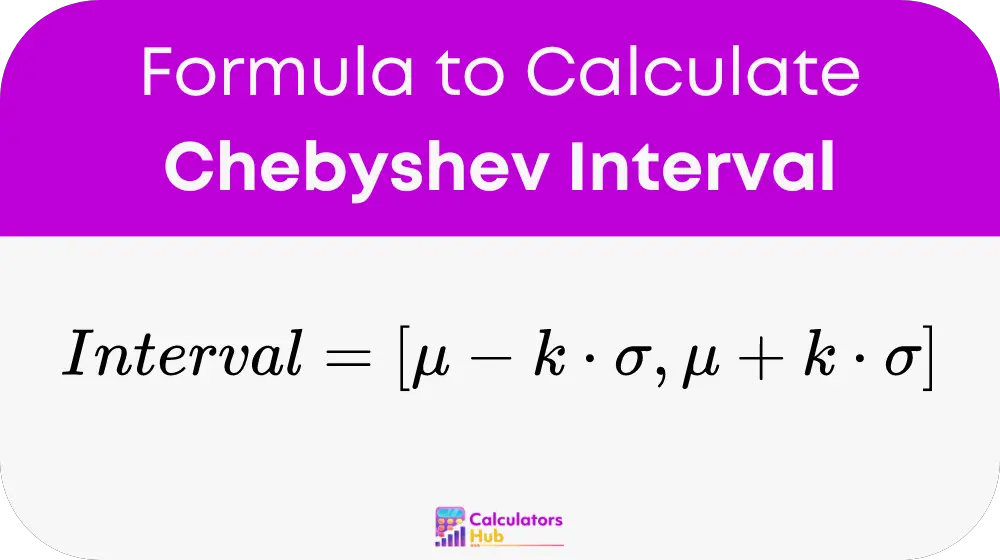
where:
- mu is the mean of the dataset.
- sigma is the standard deviation of the dataset.
- k is the number of standard deviations from the mean.
For a given percentage p, the value of k can be determined using the formula: k = sqrt( 1 / ( 1 - p ) )
For example, to calculate the 75 percent Chebyshev interval, set p = 0.75: k = sqrt( 1 / ( 1 - 0.75 ) ) = sqrt( 4 ) = 2
Therefore, for a 75 percent Chebyshev interval: Interval = [ mu - 2 * sigma, mu + 2 * sigma ]
In summary, the formula for the 75 percent Chebyshev interval is: Interval = [ mu - 2 * sigma, mu + 2 * sigma ]
Pre-calculated Intervals Table
To make it easier for users, here is a table of common Chebyshev intervals without needing to perform calculations each time:
| Percentage | k Value | Interval Formula |
|---|---|---|
| 50% | 1.414 | mu ± 1.414 * sigma |
| 75% | 2 | mu ± 2 * sigma |
| 90% | 3.162 | mu ± 3.162 * sigma |
| 95% | 4.472 | mu ± 4.472 * sigma |
| 99% | 10 | mu ± 10 * sigma |
Example of 75 Chebyshev Interval Calculator
Let's go through an example to illustrate the calculation:
Suppose we have a dataset with a mean (mu) of 50 and a standard deviation (sigma) of 5. We want to find the 75 percent Chebyshev interval.
- Calculate k for 75 percent: k = sqrt( 1 / ( 1 - 0.75 ) ) = sqrt( 4 ) = 2
- Determine the interval: Interval = [ 50 - 2 * 5, 50 + 2 * 5 ] Interval = [ 50 - 10, 50 + 10 ] Interval = [ 40, 60 ]
Thus, 75 percent of the data points lie within the interval 40 to 60.
Most Common FAQs
Chebyshev's inequality states that for any dataset, regardless of distribution, a certain proportion of data points will fall within a specified number of standard deviations from the mean. This makes it a powerful tool for statistical analysis.
The calculator provides a quick and reliable way to determine the interval within which 75 percent of data points lie, which is useful for understanding data distribution, especially when the distribution is not normal.
Yes, Chebyshev's inequality is applicable to any dataset, regardless of its distribution shape. This makes it versatile for various statistical analyses.