The Catenary Equation Calculator is a specialized tool used to determine the shape of a hanging cable or chain under its own weight. This curve, known as a catenary, appears in various applications, such as suspension bridges, power lines, and decorative arches. The calculator provides users with the ability to model and analyze the catenary shape based on specific parameters, making it essential for engineers, architects, and anyone involved in structural design.
Understanding the catenary is crucial in many fields, as it helps in predicting how materials will behave under certain loads. By accurately calculating the shape of the catenary, professionals can ensure the structural integrity and aesthetic appeal of their designs.
Formula of Catenary Equation Calculator
The catenary curve can be described by the equation:
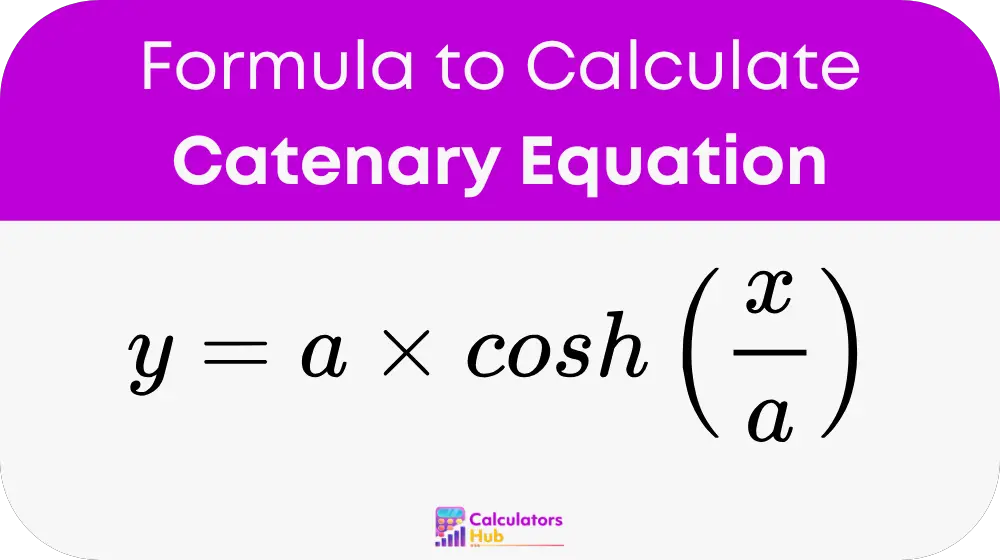
where:
- y = vertical position of the catenary at horizontal distance x (in meters)
- x = horizontal distance from the lowest point of the catenary (in meters)
- a = parameter related to the horizontal tension in the cable and the weight per unit length of the chain or cable (in meters)
- cosh = hyperbolic cosine function
This formula allows users to understand how the catenary's shape changes based on the parameters inputted, providing a clear representation of the curve's form.
Common Search Terms and Calculator
The following table includes general terms and values that people commonly search for when using a Catenary Equation Calculator. This information can be useful for quick reference without the need for calculations each time.
| Term | Value | Description |
|---|---|---|
| Catenary Parameter (a) | Varies | Influences the steepness and shape of the catenary curve. |
| Catenary Height (y) | Depends on (x) and (a) | The vertical height of the catenary at any horizontal distance. |
| Horizontal Distance (x) | Varies | The distance from the lowest point of the catenary. |
| 1 Meter | 1 Meter | Standard unit of measurement in the metric system. |
| Cosh Function | cosh(x) = (e^x + e^(-x)) / 2 | The hyperbolic cosine function used in the catenary equation. |
This table serves as a handy reference for understanding how various units relate to catenary calculations.
Example of Catenary Equation Calculator
For instance, if the parameter aaa is set to 5 meters and you want to calculate the vertical position of the catenary at a horizontal distance of 3 meters, you would use the formula:
y = a * cosh(x / a)
Plugging in the values:
y = 5 * cosh(3 / 5)
Calculating the hyperbolic cosine function gives:
y ≈ 5 * 1.1 = 5.5 meters
Thus, the vertical position of the catenary at 3 meters from its lowest point is approximately 5.5 meters.
Most Common FAQs
A catenary curve is the shape that a flexible chain or cable assumes when suspended by its ends and acted upon by a uniform gravitational force. It is distinct from a parabola, although they may look similar in some cases.
The parameter 'a' represents the horizontal tension in the cable relative to its weight. A larger value of 'a' results in a flatter catenary, while a smaller value produces a steeper curve.
Yes, the calculator can be applied to different materials as long as the weight per unit length is known. This allows for accurate modeling of how various cables and chains behave under load.