The Electrical Force Calculator computes the force between two charged particles using Coulomb’s law. This law states that the electrical force (F) between two charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. By inputting the values of the charges and the distance, the calculator provides the magnitude of the electrical force in Newtons (N).
Formula of Electrical Force Calculator
The formula used by the Electrical Force Calculator is:
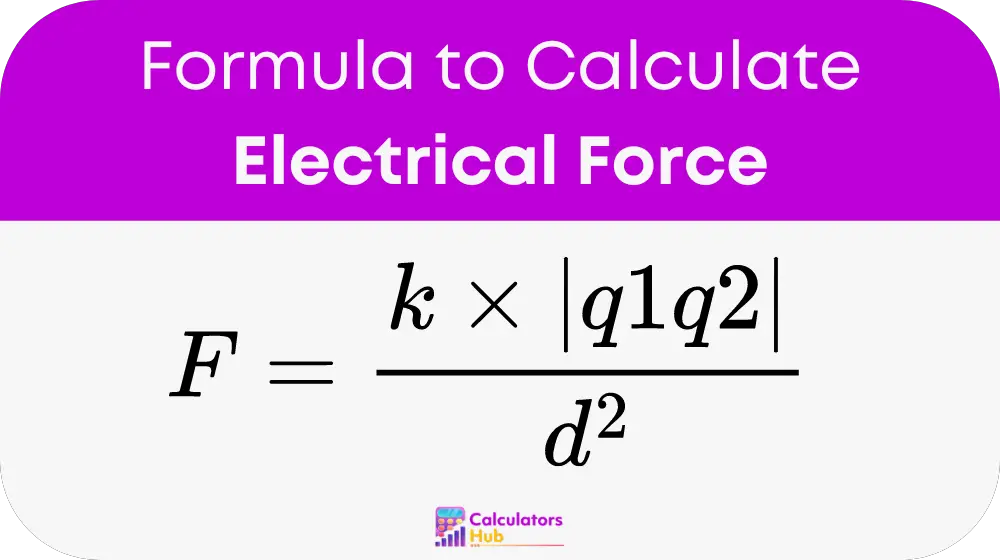
where:
- F is the magnitude of the electrical force (in Newtons, N)
- k is the Coulomb constant, approximately equal to 8.988 x 10^9 N⋅m²/C²
- q1 and q2 are the charges of the two particles (in Coulombs, C)
- d is the distance between the centers of the two particles (in meters, m)
This formula takes into account the magnitude of the charges and the distance between them to calculate the force exerted.
Common Terms and Conversions
| Term | Description | Conversion |
|---|---|---|
| Coulomb (C) | Unit of electric charge | 1 C = 6.242 x 10^18 elementary charges |
| Newton (N) | Unit of force | 1 N = 1 kg⋅m/s² |
| Meter (m) | Unit of distance | 1 m = 100 cm |
This table provides quick reference for common terms and conversions related to electrical force calculations.
Example of Electrical Force Calculator
Let’s walk through an example of how to use the Electrical Force Calculator:
- Determine the charges and distance: Suppose you have two charges, q1 = 2 x 10^-6 C and q2 = 3 x 10^-6 C, and they are 0.05 meters apart.
- Input the values into the formula: F = 8.988 x 10^9 * |2 x 10^-6 * 3 x 10^-6| / 0.05^2
- Calculate the result: F = 8.988 x 10^9 * 6 x 10^-12 / 0.0025 = 21.57 N
In this example, the electrical force between the two charges is 21.57 Newtons.
Most Common FAQs
The Coulomb constant (k) is a value used in the calculation of electrical force between two charges. It is approximately 8.988 x 10^9 N⋅m²/C² and accounts for the permeability of free space.
The electrical force is inversely proportional to the square of the distance between the charges. This means that as the distance increases, the force decreases rapidly.
Yes, the calculator can handle negative charges. The formula uses the absolute value of the product of the charges, so the sign of the charge does not affect the magnitude of the force.