The Dopant Concentration Vs Resistivity Calculator helps users determine the electrical resistivity of a semiconductor material based on the concentration of dopants. This tool is particularly useful for engineers, scientists, and researchers working in the field of semiconductor physics and electronic device manufacturing. By inputting the dopant concentration and carrier mobility, the calculator provides the resistivity value, which is essential for designing electronic components such as transistors, diodes, and integrated circuits.
Formula
The relationship between dopant concentration and resistivity in a semiconductor is given by the equation:
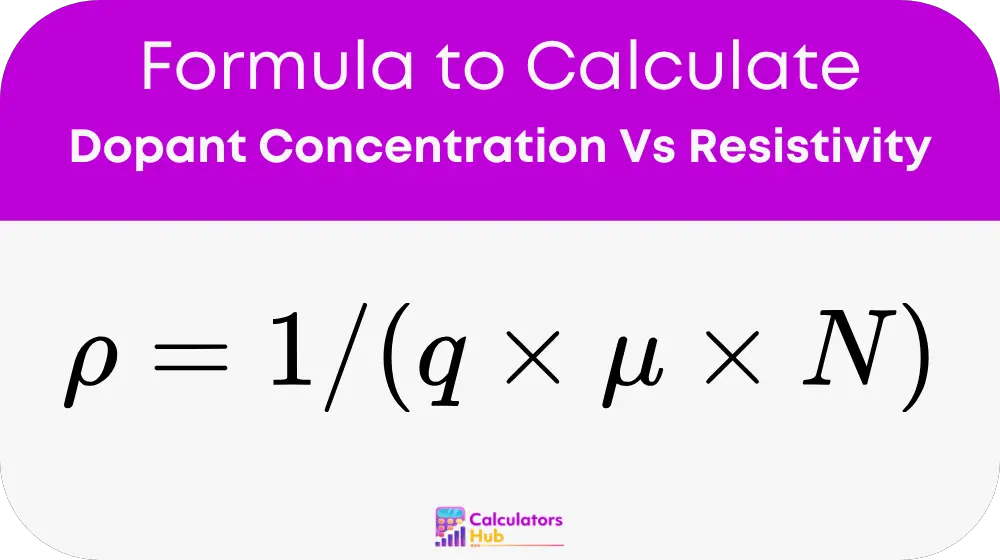
Where:
- ρ = Resistivity (Ω·cm)
- q = Elementary charge (1.602 × 10⁻¹⁹ C)
- μ = Carrier mobility (cm²/V·s)
- N = Dopant concentration (atoms/cm³)
This equation illustrates that resistivity decreases as the dopant concentration increases, assuming carrier mobility remains constant.
Commonly Used Values Table
The table below provides reference values for different semiconductor materials and their typical dopant concentrations and resistivities:
| Material | Dopant Type | Carrier Mobility (cm²/V·s) | Typical Dopant Concentration (atoms/cm³) | Resistivity (Ω·cm) |
|---|---|---|---|---|
| Silicon (Si) | P-type (B) | 450 | 1 × 10¹⁵ | 0.44 |
| Silicon (Si) | N-type (P) | 1350 | 1 × 10¹⁵ | 0.15 |
| GaAs | N-type (Si) | 8500 | 5 × 10¹⁶ | 0.002 |
| Germanium (Ge) | P-type (Ga) | 1900 | 1 × 10¹⁴ | 4.2 |
These values can be used as a quick reference to estimate resistivity without performing detailed calculations.
Example Calculation
Problem: Calculate the resistivity of an N-type silicon semiconductor with a dopant concentration of 5 × 10¹⁶ atoms/cm³ and a carrier mobility of 1350 cm²/V·s.
Solution:
Using the formula:
ρ = 1 / (q × μ × N)Substituting the given values:
ρ = 1 / (1.602 × 10⁻¹⁹ × 1350 × 5 × 10¹⁶)ρ = 1 / (1.08135 × 10⁴)ρ ≈ 9.25 × 10⁻⁵ Ω·cmThus, the resistivity of the given semiconductor material is 0.0000925 Ω·cm.
Most Common FAQs
When more dopant atoms are added, more charge carriers become available in the material. This increases electrical conductivity, thereby decreasing resistivity.
Temperature influences carrier mobility. As temperature increases, phonon scattering increases, reducing carrier mobility and increasing resistivity.
This formula is primarily applicable to extrinsic semiconductors in their low-to-moderate doping ranges. At extremely high doping concentrations, additional effects like bandgap narrowing and carrier scattering may require more complex models.